Linear Programming
This section is part of Discrete Mathematics. If you do not study that, you may not need to learn this.
An introductory example
Section titled “An introductory example”A factory produces two types of drink: an energy drink and a refresher drink. The day’s output is to be planned. Each drink requires syrup, vitamin supplement and concentrated flavouring, as shown in the table. The last row in the table show how much of each ingredient is available for the day’s production.
| Drink Type | Syrup (litres) | Vitamin Supplement (units) | Concentrated Flavouring (cc) |
|---|---|---|---|
| Energy Drink (5l) | 3 | 2 | 30 |
| Refresher Drink (5l) | 1.25 | 1 | 20 |
| Available | 250 | 300 | 30 |
- Energy drinks sell for £1 per litre.
- Refresher drinks sell for £0.80 per litre.
- let
represent the litres of energy drink that can be produced. - let
represent the litres of refresher drink that can be produced.
Syrup constraint:
Section titled “Syrup constraint:”Constraints
Section titled “Constraints”Objective function
Section titled “Objective function”.
We have now formulated the linear programming problem.
Solving
Section titled “Solving”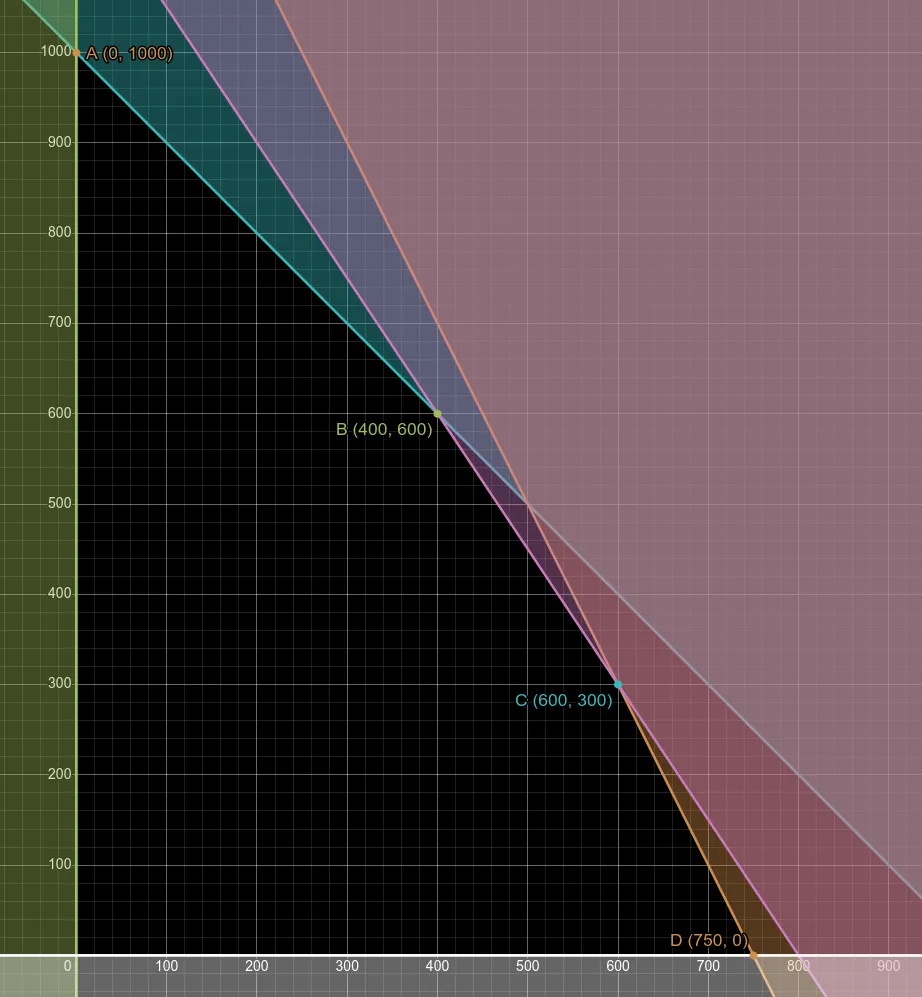
- A:
, : - B:
, : - C:
, : - D:
, :
The maximum profit is £880 at point B, where 400 litres of energy drink and 600 litres of refresher drink are produced.
Another example
Section titled “Another example”A factory produces two toys: a bicycle and a truck. Each toy requires time on a lathe and time on an assembler, as shown in the table. The last row in the table shows how much time is available on each machine for the day’s production.
| Toy Type | Lathe (hours) | Assembler (hours) |
|---|---|---|
| Bicycle | 2 | 2 |
| Truck | 1 | 3 |
| Available | 16 | 12 |
Constraints
Section titled “Constraints”(lathe) (assembler)
Objective function
Section titled “Objective function”We have now formulated the linear programming problem.
A third example
Section titled “A third example”A wall is to be built using two types of bricks of equal thickness. The wall is to be 3 metres high, 100 metres long and the thickness of a single brick. The large type of brick is of height 10cm and length 20cm. The small type of brick is of height 5cm and length 10cm.
Ignoring the mortar between the bricks, the constraint
represents the number of large bricks used. represents the number of small bricks used. - Each large brick has a face area of
, or . - Each small brick has a face area of
. - So the large bricks are 4 times the area of the small bricks.
- The total area of the wall is
. - This means that the total area of the bricks must be at least
. - Therefore, the constraint
. - This constraint is equivalent to
when both sides are multiplied by 200.
Each large brick needs 0.5 litres of mortar. Each small brick requires 0.25 litres of mortar.
Given that 10000 litres of mortar are available, write down a constraint for the number of large and small bricks that can be used.
. - Simplifies to
Large bricks cost 25p each to produce, and small bricks cost 5p each to produce. Formulate a linear programming to find how many bricks of each type should be used to build the wall as cheaply as possible.
- Let
represent the number of large bricks used. - Let
represent the number of small bricks used. - Constraints:
- Objective function:
We have now formulated the linear programming problem.
Use a graphical method to solve this. Interpret your solution.
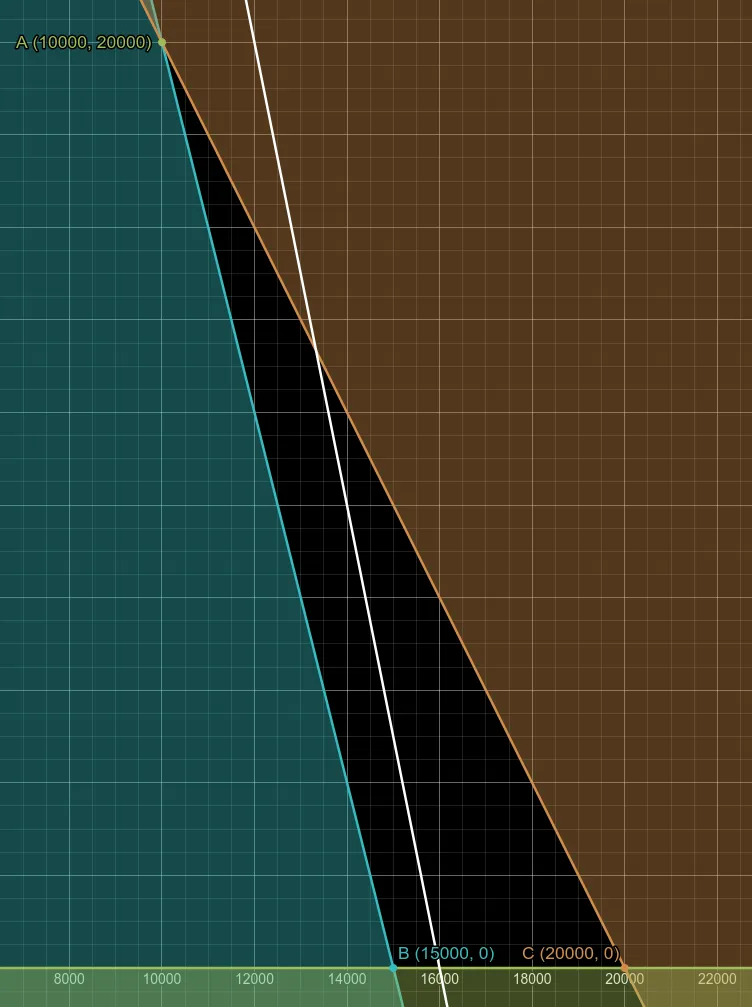
- A:
, : - B:
, : - C:
, :
The cheapest way to build the wall is to use 10000 large bricks and 20000 small bricks, which will cost £3500.
A fourth example
Section titled “A fourth example”A landscaping project is being planned to cover an area of
- Let
represent the number of trees planted. - Let
represent the number of shrubs planted.
Objective function
Section titled “Objective function”- Maximise
.
Constraints
Section titled “Constraints”(can’t have negative trees) (minimum 75 shrubs) (space) (budget)
We have now formulated the linear programming problem.
Solving
Section titled “Solving”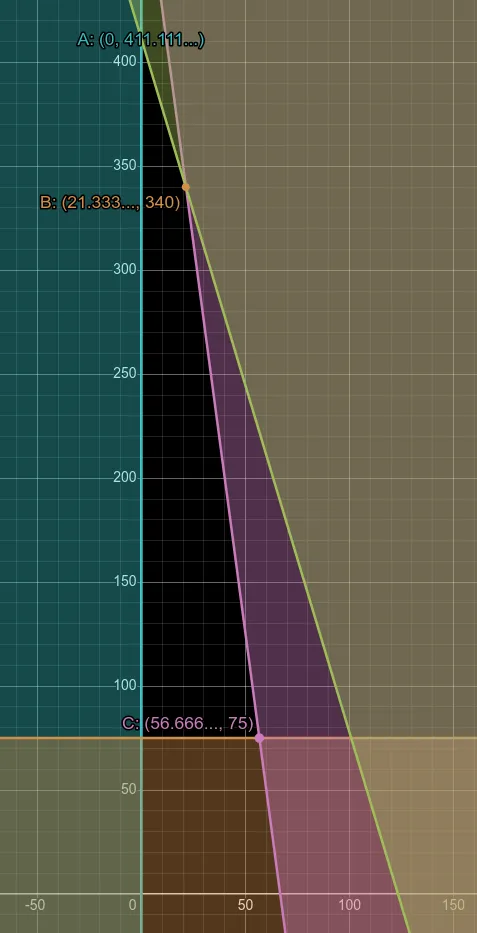
- A:
, (but we can only have whole shrubs, so ): - B:
, (but we can only have whole trees, so ): - C:
, (but we can only have whole trees, so ):
The maximum environmental benefit is 445 (arbitrary units) at point B. This involves planting 21 trees and 340 shrubs.
A more optimal solution?
Section titled “A more optimal solution?”Because we rounded down the number of trees, it is now possible that we could fit some more shrubs into the budget and space available. We have to check this to ensure that our solution is optimal.
- With 21 trees, we have used £630 of the budget and
of space. - This leaves £3070 and
for shrubs. - Each shrub costs £9 and requires
of space. - The budget allows for a maximum of
shrubs. - The space allows for a maximum of
shrubs. - Therefore, we can afford to plant 341 shrubs.
Aha! We can plant another shrub, increasing our environmental benefit to
You need to consider this in linear programming problems where the values are not integers. In exams, it is unlikely that you will be given a problem where this can happen, but it is worth being aware of.